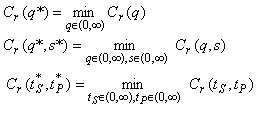Abstract:
The work is a generalization of three Wilson's models related with the gestion (management) of stocks in the deterministic case. A new variable r, called stock rate or simulation rate, appears in all models. This variable assures a better stock controlling by deterministic simulation method. For r = 1/2 we obtain all Wilson's results from the bibliography [4], [5]. For each economical model the mathematical foundation is given, together with several numerical applications and economical interpretations. All models are based on the same notations with their specific meanings. So we used the following notations:

N = The total number of supplies
h = The period length (the number of days, let us say) between two supplies; h is constant.
c_L = The launch cost for one demand of supply (the ordering cost per one order)
c_H = The holding cost (in warehouse) unit cost, per day
c_P = The penalty cost per item, per day (when the stock s is less then the client's demand)
W = The production rate of the factory, on the unit time (the model 3)
D = The client's demand rate on the unit time (the model 3)
From time in time the manager has to stop the production activity, otherwise the whole quantity WT is too big, i.e. WT >> Q.
t_W = The working time (the production time) for the factory or industrial unit
t_S = The stop time (the factory doesn't work)
t_WP = The working time and the penalty time for the factory because the client's demands are not satisfied
t_P = The penalty time and stop time
C_r(q) = The total cost (composed of the ordering and holding cost) for interval , in model 1
C_r(q,s) = The total cost (composed of the ordering, holding and penalty cost) for interval [0,T], in model 2
C_r(t_S,t_P) = The total cost (composed of the production cost and ordering, holding and penalty cost) for the interval [0,T], in model 3
In the above description the elements T, Q, W, D, c_L, c_H, c_P and r are input data
The elements q, s, N, h, t_S, t_P, t_W, t_WP are unknown data (positive real numbers). They must be found by using the mathematical models for the maintenance stock problem
The aim of the stock theory is to determine the best values q* (model 1), q*, s* (model 2), t_S*, t_P* (model 3) which minimize the total maintenance costs, respectively

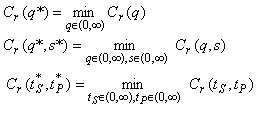
Each mathematical model generates an informatics model and a C++ program. So, the work contains three C++ valid programs: source codification, numerical output results and print screen. The C++ simulation programs have been validated by supplementary techniques and independent computations. By simulation with various values of r a good manager has the possibility to choose the best version of his activity.

Brief Biography of the Speaker:
Popoviciu Nicolae is PhD in mathematics (from 1976), professor at Hyperion University of Bucharest, Romania, Faculty of Mathematics-Informatics and the dean of this faculty. His area of competence contains: stochastic processes and Markov decision problems, integral transforms (continuous, discrete, fast Fourier transform, discrete Fourier transform), complex functions, field theory, distribution theory, tensor computation, mathematical programming (linear, multi-objective, quadratic, convex, nonlinear, stochastic, in integer numbers, Boolean) and optimization models, artificial neural networks and applications. He is the first author of 18 books (all in Romanian language) and 102 papers (almost all in English language) and more exactly the first author of 89 papers. His recently book Neural Networks. Mathematical Foundation, Algorithms and Applications (2009, Romanian language) is a monograph on the algorithms of neural networks with application.
Professor Popoviciu is member of Romanian Society of Mathematics and member of the Romanian Probability and Statistics Society. He has participated to many WSEAS International Conference: plenary speaker, author, co-author, chairman, reviewer etc (Romania, Greece, Turkey, Bulgaria, United Kingdom, USA ).