|
|
Plenary
Lecture
Geometrical Approach of Multidimensional Linear Systems

Professor Valeriu Prepelita
University Politehnica of Bucharest
Department of Mathematics Informatics
Romania
Email:
vprepelita@mathem.pub.ro
Abstract:
The
Geometric Approach is an important trend in Systems and
Control Theory developed to achieve a better and deaper
investigation of the structural properties of linear
dynamical systems and to provide efficient and elegant
solutions of problems of controller synthesis such as
decoupling and pole-assignment problems or the
compensator and regulator synthesis for linear
time-invariant multivariable systems.
The Geometric approach provides a very clear
concept of minimality and explicit geometric conditions
for controllability, observability, constructibility,
pole assignability, tracking or regulation etc. The
fundaments of this approach are some invariant
subspaces with respect to a linear transformation.
In 1969 Basile and Marro introduced and studied the
basic geometric tools named by them controlled
and conditioned invariant subspaces which were
applied to disturbance rejection or unknown-input
observability. In 1970 Wonham and Morse applied a
maximal controlled invariant method to decoupling and noninteracting control problems and later on Wonham's
book imposed the name of "(A,B)-invariant" instead
of "(A,B)-controlled invariant". Basile and Marro opened new prospects to many applications (disturbance rejection,
noninteraction etc.) by the robust controlled invariant
and the emphasis of the duality. Other properties analysed using geometric tools are invertibility,
functional controllability or unknown input
observability The LQ problem was also studied in a
geometric framework by Silverman, Hautus and Willems.
J.C. Willems also developed the theory of almost
controlled and almost conditioned invariant subspaces
used in high-gain feedback problems. Further
contributions are due to numerous researchers among
which Anderson, Akashi, Bhattacharyya, Kucera, Malabre,
Molinari, Pearson, Francis and Schumacher. The range of
the applications of the Geometric approach was extended
to various areas, including, for instance, Markovian
representations (Lindquist, Picci and Ruckebusch)
or modeling and estimation of linear stochastic systems).
The past three decades have seen a continually growing
interest in the theory of two-dimensional (2D) or, more
generally, multidimensional (nD) systems, which
become a distinct and important branch of the systems
theory. The reasons for the interests in
this domain are on one side the richness in potential
application fields and on the other side the richness
and significance of the theoretical approaches. The
application fields include circuits, control and signal
processing, image processing, computer tomography,
gravity and magnetic field mapping, seismology, control
of multipass processes, etc.
A quite new field of the $n$D systems theory is
represented by the 2D hybrid models, whose state
equation is of differential-difference type. These hybrid models
have applications in various areas such as linear
repetitive processes, pollution modelling, long-wall
coal cutting and metal rolling or in iterative learning
control synthesis.
In the present paper, a class of multidimensional hybrid
systems described by differential-difference state
equations is studied from the point of view of the
geometric approach. The state space representation of
these systems is given: a multidimensional hybrid
systems is given by a set 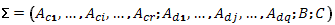 where where
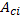 and and
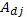 are
the are
the 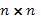 continuous-time
and discrete-time drift matrices, continuous-time
and discrete-time drift matrices, 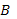 is
the is
the 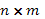 input-state
matrix, input-state
matrix, 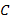 is
the is
the 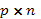 state-output
matrix and state-output
matrix and 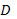 is
the is
the 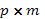 input-output
matrix. The formulas of the state as well as of the
input-output map are obtained. The considered systems
represent extensions to multidimensional hybrid
continuous-discrete models of Attasi's 2D discrete-time
systems. input-output
matrix. The formulas of the state as well as of the
input-output map are obtained. The considered systems
represent extensions to multidimensional hybrid
continuous-discrete models of Attasi's 2D discrete-time
systems.
The notions of controllable and reachable states are
defined, as well as the completely controllable and the
completely reachable systems. states. A suitable
reachability Gramian is constructed for time-invariant
multidimensional systems and it is used to obtain
conditions for the phase transfer and criteria of
reachability. The controllability matrix is constructed
and it is used to characterize the space of the
reachable states as the minimal 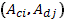 -invariant
subspace which contains the columns of the matrix B
and to obtain necessary and sufficient conditions of
reachability for multidimensional hybrid systems. -invariant
subspace which contains the columns of the matrix B
and to obtain necessary and sufficient conditions of
reachability for multidimensional hybrid systems.
An algorithm is provided which compute the minimal 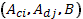 -invariant
subspace, (i.e. the subspace of the controllable states
of the system -invariant
subspace, (i.e. the subspace of the controllable states
of the system  )
and which extends the 1D algorithm from. )
and which extends the 1D algorithm from.
By duality, similar results are obtained for
the observability of the time-invariant multidimensional
systems and an algorithm is proposed which compute the
maximal 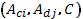 -invariant
subspace. -invariant
subspace.
Brief Biography of the Speaker:
Valeriu Prepelita graduated from the Faculty of
Mathematics-Mechanics of the University of Bucharest in
1964. He obtained Ph.D. in Mathematics at the University
of Bucharest in 1974. He is currently Professor at the
Faculty of Applied Sciences, the University Politehnica
of Bucharest, Director of the Department
Mathematics-Informatics. His research and teaching
activities have covered a large area of domains such as
Systems Theory and Control, Multidimensional Systems,
Functions of a Complex Variables, Linear and Multilinear
Algebra, Special Functions, Ordinary Differential
Equations, Partial Differential Equations, Operational
Calculus, Probability Theory and Stochastic Processes,
Operational Research, Mathematical Programming,
Mathematics of Finance.
Professor Valeriu Prepelita is author of more than 110
published papers in refereed journals or conference
proceedings and author or co-author of 15 books. He has
participated in many national and international Grants.
He is member of the Editorial Board of some journals,
member in the Organizing Committee and the Scientific
Committee of several international conferences, keynote
lecturer or chairman of some sections of these
conferences. He is a reviewer for five international
journals. He received the Award for Distinguished
Didactic and Scientific Activity of the Ministry of
Education and Instruction of Romania..
|
|

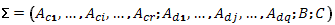 where
where